Στα πλαίσια της συμμετοχής της ομάδας RadiNOx στον διαγωνισμό CanSat διενεργήθηκε μελέτη της αντοχής του δορυφόρου κατά το άνοιγμα του αλεξίπτωτου στα 1000 m ύψος, αλλά και κατά την προσγείωση και κρούση του με το έδαφος. Η εν λόγω μελέτη πραγματοποιήθηκε με χρήση του προγράμματος πεπερασμένων στοιχείων ANSYS 19.2 (ακαδημαϊκή άδεια Ε.Μ.Π.). Στη συνέχεια θα παρατεθούν τα επιμέρους βήματα, που ακολουθήθηκαν για τη δημιουργία του μοντέλου προσομοίωσης.
ΣχεδιασμΟς μοντΕλου
Εικόνα 1 Γεωμετρία (αριστερά) και πλεγματοποίηση (meshing) (δεξιά) του δορυφόρου, που χρησιμοποιήθηκε για την προσομοίωση κατά το άνοιγμα του αλεξίπτωτου.
Εικόνα 2 Γεωμετρία (αριστερά) και meshing (δεξιά) του δορυφόρου και του εδάφους που χρησιμοποιήθηκε για την προσομοίωση κατά την προσγείωση.
ΚαθορισμΟς υλικΩν
Τα υλικά, που χρησιμοποιήθηκαν και τα βασικά του χαρακτηριστικά είναι τα ακόλουθα:
1) ABS πλαστικό για το κέλυφος του δορυφόρου.
Πυκνότητα: 1040 kg/m3
Όριο Ελαστικότητας: 2.39 GPa
2) Χάλυβας κατασκευών με μη γραμμική συμπεριφορά για τις τρεις ράβδους ένωσης των εσωτερικών μερών με το κέλυφος του δορυφόρου, έτσι ώστε να προβλεφθεί και το ενδεχόμενο πλαστικής παραμόρφωσης του μοντέλου.
Πυκνότητα: 7850 kg/m3
Όριο Ελαστικότητας: 200 GPa
Όριο Διαρροής: 250 MPa
3) Έδαφος μεσαίας πυκνότητας, το οποίο χρησιμοποιήθηκε για την προσομοίωση της στιγμής της προσγείωσης του δορυφόρου, η οποία αναμένεται να πραγματοποιηθεί σε σχετικά μαλακό έδαφος.
Πυκνότητα: 2400 kg/m3
ΜΕθοδος επΙλυσης-ΟριακΕς συνθΗκες
AντοχΗ του δορυφΟρου κατΑ το Ανοιγμα του αλεξΙπτωτου
Για το μοντέλο, στο οποίο μελετάται η αντοχή του δορυφόρου κατά το άνοιγμα του αλεξίπτωτου, χρησιμοποιήθηκε η λειτουργία “Static structural” του ANSYS, με τις οριακές συνθήκες να διακρίνονται στην Εικόνα 3. Η δύναμη, που εφαρμόζεται στις τρεις ράβδους της κατασκευής υπολογίστηκε σύμφωνα με τον παρακάτω τύπο:
FD: Η δύναμη αντίστασης κατά το άνοιγμα του αλεξίπτωτου
Cd: Ο συντελεστής αντίστασης του αέρα (με βάση τον τύπου του αλεξίπτωτου Cd=1.75)
ρ: Η πυκνότητα του αέρα (1.22 kg/m3)
Α: Hεπιφάνεια του αλεξίπτωτου (πd2/4, d=248mm)
Vτ: Η τελική ταχύτητα του δορυφόρου
m: Η μάζα του δορυφόρου (περίπου 0.144 kg)
g: Η επιτάχυνση της βαρύτητας (9.81 m/s^2)
ρ: Η πυκνότητα του αέρα (1.22 kg/m^3)
Cd: Ο συντελεστής αντίστασης του αέρα (όπως αυτός προκύπτει από το σχήμα της βάσης του αλεξίπτωτου Cd=0.85)
Α: H επιφάνεια της βάσης του δορυφόρου [(πd^2)/4, d=66mm]
Μετά τους υπολογισμούς προέκυψε ότι Vτ=28.24 m/s (101.66 km/h) και FD=41.1 N , η οποία τιμή της δύναμης δια του τρία εφαρμόστηκε σε κάθε μια από τις ράβδους του δορυφόρου, όπως διακρίνεται και στην Εικόνα 3. Πρέπει να σημειωθεί ότι η συγκεκριμένη ταχύτητα χρησιμοποιείται στον υπολογισμό της δύναμης FD ως ακραία περίπτωση ελέγχου της δομικής ακεραιότητας του δορυφόρου κατά το άνοιγμα του αλεξίπτωτου. Κι αυτό, γιατί υπό κανονικές συνθήκες το αλεξίπτωτο θα ανοίξει σε σύντομο χρονικό διάστημα από την στιγμή, που θα αφεθεί ο δορυφόρος από το ύψος των 1000 m και, επομένως, η τιμή της ταχύτητας θα είναι κατά πολύ μικρότερη από την vT και κατ’ επέκταση και η FD.
ΑντοχΗ του δορυφΟρου κατΑ την προσγεΙωση
Σε ό,τι αφορά το μοντέλο για την μελέτη της αντοχής του δορυφόρου κατά την προσγείωση χρησιμοποιήθηκε η λειτουργία “Explicit Dynamics” του ANSYS, με τις οριακές συνθήκες να διακρίνονται στην Εικόνα 4 και στην Εικόνα 5. Ως προς τις ταχύτητες προσγείωσης μελετήθηκαν τρεις περιπτώσεις με v=1.5 m/s (5.4 km/h), v=3.5 m/s (12.6 km/h), v=6 m/s (21.6 km/h) και v=10 m/s (36 km/h), έτσι ώστε να καθοριστούν τα αποτελέσματα που επιφέρει η διαφορετική ταχύτητα στην δομική ακεραιότητα του δορυφόρου.
Εικόνα 4 Καθορισμός ταχύτητας πτώσης του δορυφόρου.
Εικόνα 5 Οριακές συνθήκες μοντέλου δορυφόρου και εδάφους.
ΑποτελΕσματα επΙλυσης
ΑντοχΗ του δορυφΟρου κατΑ το Ανοιγμα του αλεξΙπτωτου
Εικόνα 6a Ολική παραμόρφωση του δορυφόρου.
Εικόνα 8a Ελαστική παραμόρφωση του δορυφόρου.
Εικόνα 7a Ελαστικές τάσεις στον δορυφόρο.
Εικόνα 9a Πλαστική παραμόρφωση του δορυφόρου.
ΑντοχΗ του δορυφΟρου κατΑ την προσγεΙωση
Στη συνέχεια ακολουθούν τα αποτελέσματα από την επίλυση και των δύο μοντέλων, τα οποία περιλαμβάνουν την ολική παραμόρφωση (total deformation), τις ελαστικές τάσεις (elastic stress), την ελαστική παραμόρφωση (elastic strain) και την πλαστική παραμόρφωση (plastic strain).
v=1.5 m/s
Εικόνα 10a Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 12a Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 11a Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 13a Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=3.5 m/s
Εικόνα 14a Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 16a Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 15a Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 17a Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=6 m/s
Εικόνα 18a Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 20a Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 19a Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
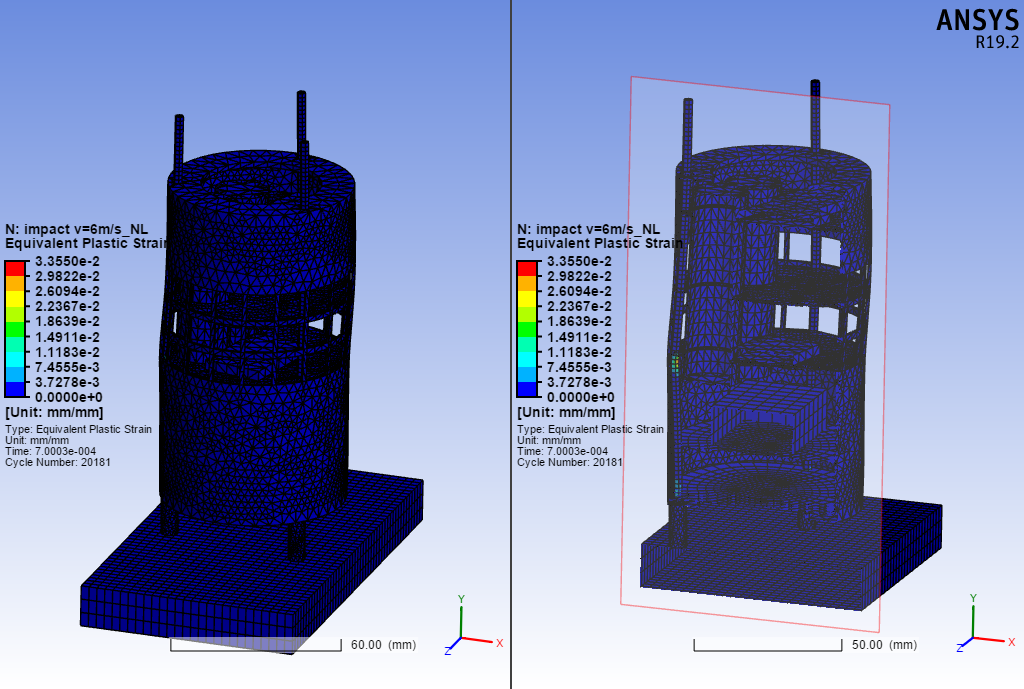
Εικόνα 21a Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=10 m/s
Εικόνα 22a Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 24a Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
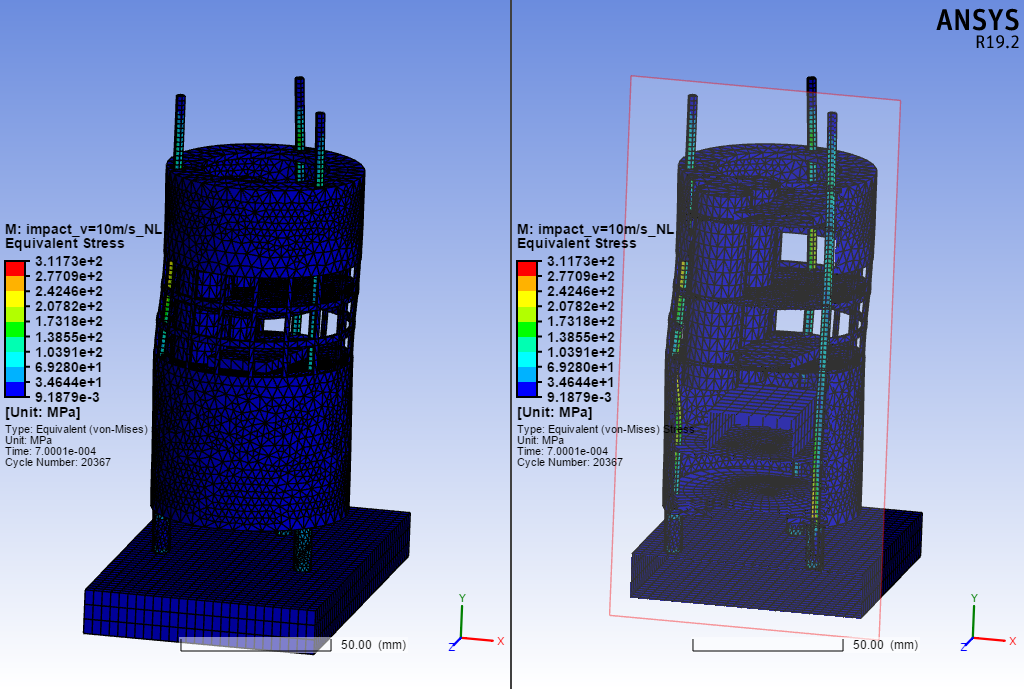
Εικόνα 23a Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 25a Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Συμπερασματα
Ακόμα και στην ακραία περίπτωση όπου η ταχύτητα του δορυφόρου κατά το άνοιγμα του αλεξίπτωτου είναι
vT=28.24 m/s η δύναμη που ασκείται στις τρεις ράβδους του δορυφόρου δεν είναι ικανή να προκαλέσει κάποια σημαντική παραμόρφωση ή αστοχία υλικού.
Εκτός από την περίπτωση στην οποία η ταχύτητα πτώσης του δορυφόρου είναι 1.5 m/s κι όπου δεν υφίστανται πλαστική παραμόρφωση τα μεταλλικά μέρη του δορυφόρου, σε όλες τις άλλες ταχύτητες παρατηρείται αυξανόμενη πλαστική παραμόρφωση καθώς αυξάνεται η ταχύτητα πτώσης.
Αντίστοιχη μελέτη διενεργήθηκε για κράμα χαλκού με μη γραμμική συμπεριφορά για τις τρεις ράβδους ένωσης των εσωτερικών μερών με το κέλυφος του δορυφόρου, έτσι ώστε να προβλεφθεί το ενδεχόμενο πλαστικής παραμόρφωσης του μοντέλου με αυτήν την επιλογή υλικού.
Πυκνότητα: 8300 kg/m3
Όριο Ελαστικότητας: 110 Gpa
Όριο Διαρροής: 280 Mpa
ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΠΙΛΥΣΗΣ
ΑΝΤΟΧΗ ΤΟΥ ΔΟΡΥΦΟΡΟΥ ΚΑΤΑ ΤΟ ΑΝΟΙΓΜΑ ΤΟΥ ΑΛΕΞΙΠΤΩΤΟΥ
Εικόνα 6b Ολική παραμόρφωση του δορυφόρου.
Εικόνα 8b Ελαστική παραμόρφωση του δορυφόρου.
Εικόνα 7b Ελαστικές τάσεις στον δορυφόρο.
Εικόνα 9b Πλαστική παραμόρφωση του δορυφόρου.
ΑΝΤΟΧΗ ΤΟΥ ΔΟΡΥΦΟΡΟΥ ΚΑΤΑ ΤΗΝ ΠΡΟΣΓΕΙΩΣΗ
Στη συνέχεια ακολουθούν τα αποτελέσματα από την επίλυση και των δύο μοντέλων, τα οποία περιλαμβάνουν την ολική παραμόρφωση (total deformation), τις ελαστικές τάσεις (elastic stress), την ελαστική παραμόρφωση (elastic strain) και την πλαστική παραμόρφωση (plastic strain).
v=1.5 m/s
Εικόνα 10b Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 12b Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 11b Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 13b Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=3.5 m/s
Εικόνα 14b Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 16b Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 15b Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 17b Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=6 m/s
Εικόνα 18b Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 20b Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 19b Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 21b Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
v=10 m/s
Εικόνα 22b Ολική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 24b Ελαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 23b Ελαστικές τάσεις στον δορυφόρο, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
Εικόνα 25b Πλαστική παραμόρφωση του δορυφόρου, όπου στην δεξιά πλευρά διακρίνεται το εσωτερικό του.
ΣυμπερΑσματα
Από τα παραπάνω αποτελέσματα είναι εμφανές ότι το μοντέλο επιδέχεται μεγαλύτερη καταπόνηση ή απ' ότι με τον χάλυβα. Συνεπώς, αυξάνεται η πιθανότητα το υλικό κατασκευής του κελύφους να αστοχήσει στην κρούση κατά τη διάρκεια της προσγείωσης.